Quaternions and Cubing

Rubik’s Cubes and Quaternion Rotations

I solve the Rubik’s Cube… uhh pretty fast I guess. Clearly not as fast as other people around the world. But speedcubing is something I’ve become really fond of. I’ve been playing with a Rubik’s Cube ever since 8th grade, and I’ve attended a few competitions, and met different kinds of people.

This was such an interesting project to work on. I learnt so many cool things doing this. The concepts of 3-D geometry and Vector Algebra are just.. *chef’s kiss* beautiful.

I generated a few images of my own, using this tool.

How I came across this problem

There was a challenge in AIcrowd that required estimating the amount of rotation, i.e., calculating the angle of rotation along the X, Y, and Z axes through regression.

After reading up a bit about rotations, and how they work in real life, I found out that this wasn’t the right question to be asking. This method of calculating angles of rotation (Euler angles) along 3 axes encounters a problem, called The Gimbal Lock.

Esentially, as a consequence of the Gimbal Lock problem, the object cannot rotate in 3 Dimensions, along all 3 axes. This problem arises when two of the three axes are aligned in parallel.

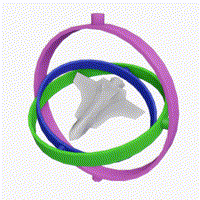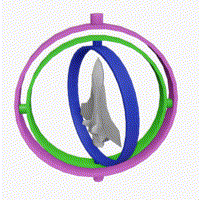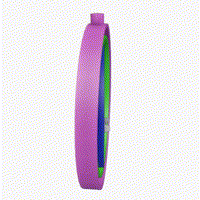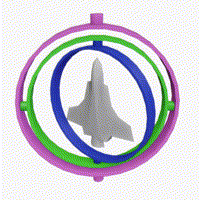
Here, you can see that the rotation along the blue axis is limited to only 2 dimensions, whereas the rotations along the pink and green axes is pretty random (in 3 dimensions).

What the solution to this is

Quaternions are a simple way to represent complex rotations, algebraically. A Quaternion can be represented in 4 Dimensions. It consists of a unit vector, and the angle of rotation along that vector.

So, any rotation that you can imagine of… In the end, the object’s final orientation can be represented by its axis of rotation, and the angle by which it rotated around that axis.

Yes. Even the worst possible rotations are still manageable!

An epiphany, and how I did this

First, I ran a Grid Detection algorithm using OpenCV, and drew the contours for each sticker, and calculated the centroids for all of them.

Since the colours are solid, I can run a simple distance measure based algorithm to find out the adjacent edge (the purple line).

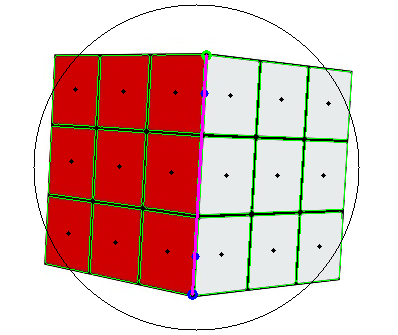
You must be wondering why the image has a circle drawn on it. That’s the best part! ANY rotation that is applied to this cube, happens within a sphere, around the core. This epiphany was what made everything click together. With the X and Y coordinate of any corner point, I can calculate the Z-coordinate, because that corner point will satisfy the equation of a point lying on a sphere of unit radius.

So, you have a line segment in 3-D. And you know the initial orientation of the same line. It’s only a few quaternion calculations to get the entire quaternion!

Neural Nets aren’t too bad

A Neural Net that takes the 3d coordinates of cube corners, and visible colors as input can be used to calculate the quaternion.

But, when simple 3D geometry and linear algebra does the trick, why bother?